Fuzzy Tiling Activations

Introduction

In the realm of artificial intelligence and machine learning, the pursuit of developing intelligent systems that can adapt and learn from new information resembles the human capacity for continuous learning. However, a challenge known as catastrophic interference [1] emerges as a critical hurdle on this path. Catastrophic interference occurs when the integration of new information disrupts or erases previously learned knowledge. Understanding and mitigating catastrophic interference is an essential pursuit, as it holds the key to creating resilient, lifelong learning systems that can flexibly acquire and retain knowledge across diverse tasks.

Recent studies suggest that sparse representations can mitigate catastrophic interference [2, 3], which arises due to the overwriting of shared network parameters when learning new tasks, which results in the loss of previously learned information. Sparse representations involve the concept of selective activation, where only a subset of neurons or features is activated for a specific task. This can alleviate catastrophic interference by limiting the extent to which new information encroaches upon existing knowledge.

[3] proposes a new approach called Online aware Meta-learning (OML), which aims to minimize interference and promote future learning by learning sparse representations that are robust and suitable for online updating in continual learning. The authors propose a meta-objective called OML that uses catastrophic interference as a training signal. They optimize the objective using gradient-based meta-learning algorithms and show that it is effective in learning representations that are more suitable for online updating in sequential regression and classification problems.

This approach encodes sparsity in the meta-learner’s objective and loss function. However, another approach could be to achieve sparsity by design, or as it is referred to in Fuzzy Tiling Activations, natural sparsity, which we are going to talk about in this blog post.

Tiling Activations

Before introducing FTA, let’s learn about a simpler version called Tiling Activation, which is the binning mechanism of FTA without smoothing. This Tiling Activation takes a scalar $z$ as input and outputs a binned vector with a value of 1 in bin corresponding to $z$ and zeros elsewhere, which is somewhat similar to one-hot encoding.

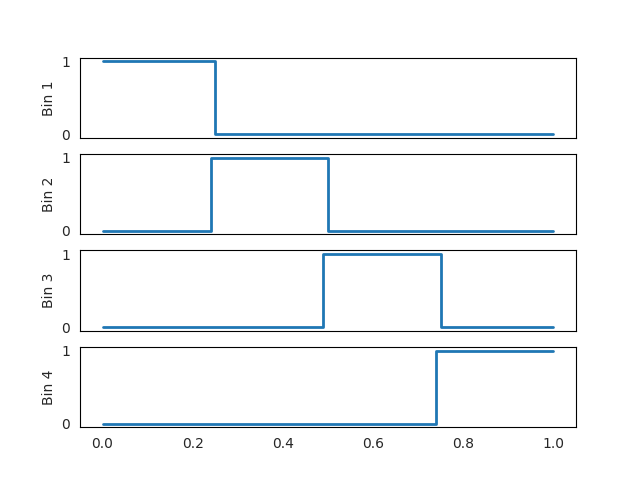Tiling activation output for k=2

In this example, the number of bins, defined as $k$, is set to 4. We passed numbers between 0 and 1 to the Tiling activation function, and as shown in this figure, for each value of $z$, the corresponding activation will be triggered.

\[\begin{cases} 0.00 \leq z < 0.25 &&& \text{bins}=\begin{bmatrix} 1&0&0&0 \end{bmatrix}\\ 0.25 \leq z < 0.50 &&& \text{bins}=\begin{bmatrix} 0&1&0&0 \end{bmatrix}\\ 0.50 \leq z < 0.75 &&& \text{bins}=\begin{bmatrix} 0&0&1&0 \end{bmatrix}\\ 0.75 \leq z < 1.00 &&& \text{bins}=\begin{bmatrix} 0&0&0&1 \end{bmatrix}\\ \end{cases}\]

Although Tiling Activation successfully generates sparse outputs, it has zero derivatives almost everywhere. This fact motivates the design of a smoother version called Fuzzy Tiling Activations.

Fuzzy Tiling Activations

FTA uses the same mechanism for binning as Tiling Activation. However, rather than sharp rises or falls, it employs ReLU-like functions for smoother transitions, resulting in non-zero derivatives. FTA introduces a parameter called $\eta$ to manage sparsity and the extent of smoothing. When $\eta = 0$, FTA becomes equivalent to Tiling Activation. A larger $\eta$ corresponds to a broader range of ReLU-like values.

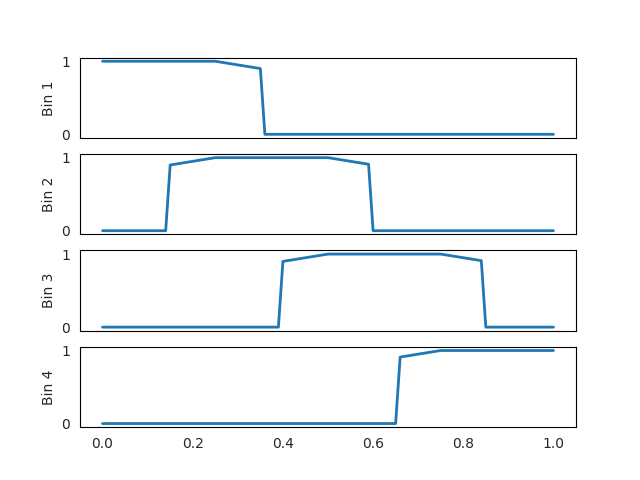FTA output for k=2, and eta=0.1

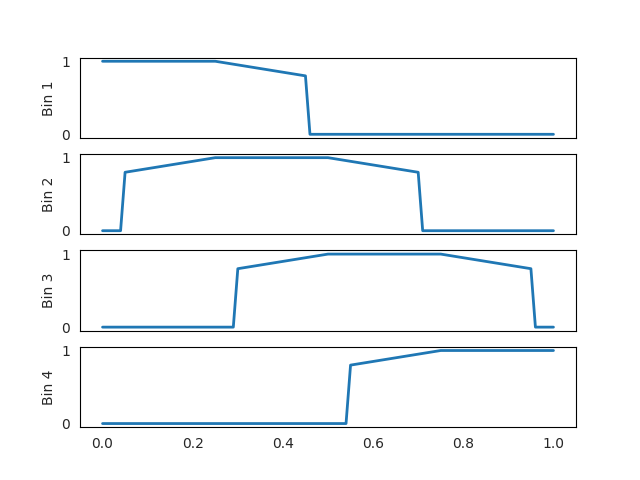FTA output for k=2, and eta=0.2

As can be observed in these figures, a larger $\eta$ leads to a broader range of ReLU-like values on both sides of the flat region.

If you wish to change these values and better understand FTA, start by cloning the original PyTorch implementation of FTA from this repository or use the version I modified for GPU usage from here. After that you can generate the plots I illustrated above by using the following code:

import torch
from fta import FTA
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
sns.set_style("whitegrid", {'axes.grid' : False,
                            'axes.edgecolor':'black'})

activation = FTA(tiles=4, bound_low=0, bound_high=1, eta=0.1, input_dim=1, device='cpu')

fig, axs = plt.subplots(4)

l = []
for i in range (0, 101):
    x = torch.tensor(i/100)
    l.append(activation(x).squeeze().numpy())

l = np.array(l)

for i in range(l.shape[1]):
    axs[i].plot(np.linspace(0, 1, l.shape[0]), l[:,i], linewidth=2)
    if i < l.shape[1]-1:
        axs[i].axes.get_xaxis().set_ticks([])
    axs[i].set(ylabel='Bin '+str(i+1))

plt.show()

Experiments

I have tested the FTA activation function in two settings: one with a simple DQN agent in the Gymnasium Taxi environment and another in a Maze environment I implemented, based on the environment introduced in [5].

Taxi environment

The code for this test is available in this repository. The results are as follows:

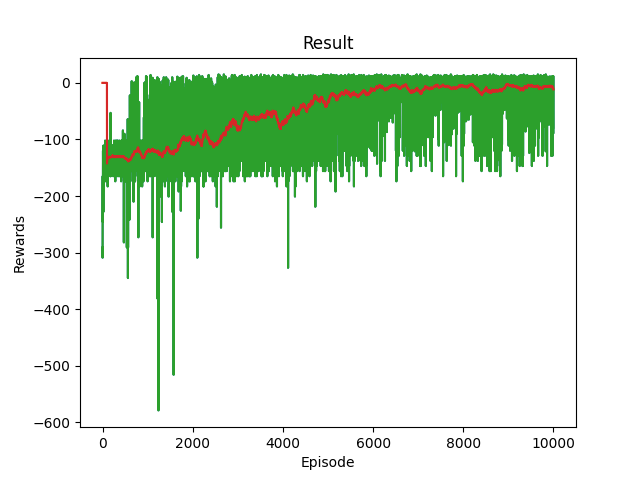Taxi env average rewards after 10000 episode by using FTA activation function.

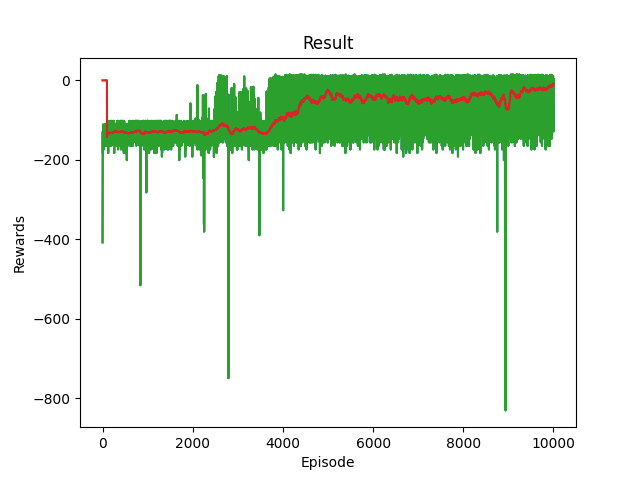Taxi env average rewards after 10000 episode by using ReLU activation function.

As illustrated in the two figures above, FTA has achieved more stable, efficient, and faster learning in comparison with the ReLU activation function.

Maze environment

FTA output for k=2, and \(\eta=0.2\)

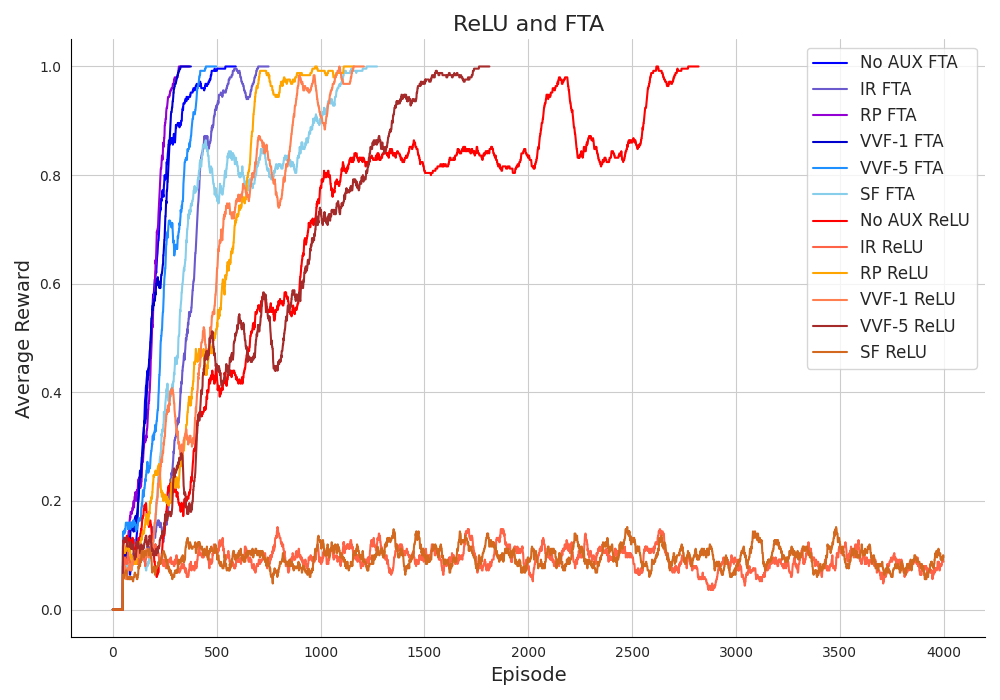
In my final bachelor project, I tried to rebuild the work introduced in [5], so I implemented a similar environment to theirs and a DQN agent with Polyak updates, along with some auxiliary tasks. The repository is available here. In a part of my experiments, I compared the usages of ReLU and FTA, as depicted in the following figure: (Note that the plots are averaged over 5 different runs and they are more accurate than the Taxi environment)

Maze env average rewards.

The FTA results are shaded in blue, while the ReLU results are illustrated in red. It is obvious that utilizing FTA could improve training by providing a more reliable and faster learning process within fewer episodes. As illustrated in this figure, FTA achieved a hundred consecutive successful episodes in a smaller number of total episodes compared to the auxiliary tasks based on ReLU.

This was only a brief introduction to FTA, where I shared my experiments. I omitted the implementation details and focused on presenting the main ideas. If you are further interested, please refer to the main article [4], and [5] could also provide valuable insights. Hope this blog was helpful to you!

References

[1] McCloskey, M., & Cohen, N. J. (1989, January 1). Catastrophic Interference in Connectionist Networks: The Sequential Learning Problem (G. H. Bower, Ed.). ScienceDirect; Academic Press. https://www.sciencedirect.com/science/article/abs/pii/S0079742108605368?via%3Dihub

[2] Liu, V., Kumaraswamy, R., Le, L., & White, M. (2018, November 15). The Utility of Sparse Representations for Control in Reinforcement Learning. ArXiv.org. https://doi.org/10.48550/arXiv.1811.06626

‌[3] Javed, K., & White, M. (n.d.). Meta-Learning Representations for Continual Learning. Retrieved August 20, 2023, from https://arxiv.org/pdf/1905.12588.pdf

‌[4] Pan, Y., Banman, K., & White, M. (n.d.). Published as a conference paper at ICLR 2021 FUZZY TILING ACTIVATIONS: A SIMPLE APPROACH TO LEARNING SPARSE REPRESENTATIONS ONLINE. Retrieved August 20, 2023, from https://arxiv.org/pdf/1911.08068v3.pdf

‌[5] Wang, H., Miahi, E., White, M., Machado, M. C., Abbas, Z., Kumaraswamy, R., Liu, V., & White, A. (2023, May 5). Investigating the Properties of Neural Network Representations in Reinforcement Learning. ArXiv.org. https://doi.org/10.48550/arXiv.2203.15955

‌ ‌

‌